Snub triapeirotrigonal tiling

Snub triapeirotrigonal tiling
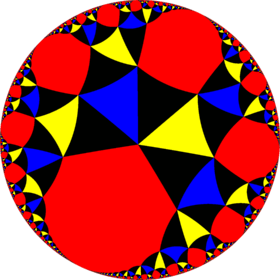Poincaré disk model of the hyperbolic plane
Type	Hyperbolic uniform tiling
Vertex configuration	3.3.3.3.3.∞
Schläfli symbol	s{3,∞} s(∞,3,3)
Wythoff symbol	| ∞ 3 3
Coxeter diagram
Symmetry group	[(∞,3,3)]+, (∞33)
Dual	Order-i-3-3_t0 dual tiling
Properties	Vertex-transitive Chiral

In geometry, the snub triapeirotrigonal tiling is a uniform tiling of the hyperbolic plane with a Schläfli symbol of s{3,∞}.

Related polyhedra and tiling

Paracompact hyperbolic uniform tilings in [(∞,3,3)] family
Symmetry: [(∞,3,3)], (*∞33)							[(∞,3,3)]+, (∞33)
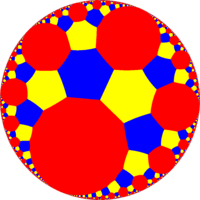(∞,∞,3)	t0,1(∞,3,3)	t1(∞,3,3)	t1,2(∞,3,3)	t2(∞,3,3)	t0,2(∞,3,3)	t0,1,2(∞,3,3)	s(∞,3,3)
Dual tilings
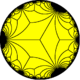V(3.∞)3	V3.∞.3.∞	V(3.∞)3	V3.6.∞.6	V(3.3)∞	V3.6.∞.6	V6.6.∞	V3.3.3.3.3.∞

References

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
• "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678. 

See also

Wikimedia Commons has media related to Uniform tiling 3-3-3-3-3-i.

• Square tiling
• Uniform tilings in hyperbolic plane
• List of regular polytopes

External links

• Weisstein, Eric W. "Hyperbolic tiling". MathWorld. 

• Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld. 

• Hyperbolic and Spherical Tiling Gallery
• KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
• Hyperbolic Planar Tessellations, Don Hatch

Tessellation
Periodic Pythagorean Rhombille Schwarz triangle Rectangle Domino Uniform tiling & honeycomb Coloring Convex Kisrhombille Wallpaper group Wythoff
Aperiodic Ammann–Beenker Aperiodic set of prototiles List Einstein problem Socolar–Taylor Gilbert Penrose Pentagonal Pinwheel Quaquaversal Rep-tile & Self-tiling Sphinx Truchet
Other Anisohedral & Isohedral Architectonic & catoptric Circle Limit III Computer graphics Honeycomb Isotoxal Packing Problems Domino Wang Heesch's Squaring Prototile Conway criterion Girih Regular Division of the Plane Regular grid Substitution Voronoi Voderberg
By vertex type Spherical 2n 33.n V33.n 42.n V42.n Regular 2∞ 36 44 63 Semi- regular 32.4.3.4 V32.4.3.4 33.42 33.∞ 34.6 V34.6 3.4.6.4 (3.6)2 3.122 42.∞ 4.6.12 4.82 Hyper- bolic 32.4.3.5 32.4.3.6 32.4.3.7 32.4.3.8 32.4.3.∞ 32.5.3.5 32.5.3.6 32.6.3.6 32.6.3.8 32.7.3.7 32.8.3.8 33.4.3.4 32.∞.3.∞ 34.7 34.8 34.∞ 35.4 37 38 3∞ (3.4)3 (3.4)4 3.4.62.4 3.4.7.4 3.4.8.4 3.4.∞.4 3.6.4.6 (3.7)2 (3.8)2 3.142 3.162 (3.∞)2 3.∞2 42.5.4 42.6.4 42.7.4 42.8.4 42.∞.4 45 46 47 48 4∞ (4.5)2 (4.6)2 4.6.12 4.6.14 V4.6.14 4.6.16 V4.6.16 4.6.∞ (4.7)2 (4.8)2 4.8.10 V4.8.10 4.8.12 4.8.14 4.8.16 4.8.∞ 4.102 4.10.12 4.122 4.12.16 4.142 4.162 4.∞2 (4.∞)2 54 55 56 5∞ 5.4.6.4 (5.6)2 5.82 5.102 5.122 (5.∞)2 64 65 66 68 6.4.8.4 (6.8)2 6.82 6.102 6.122 6.162 73 74 77 7.62 7.82 7.142 83 84 86 88 812 8.62 8.162 ∞3 ∞4 ∞5 ∞∞ ∞.62 ∞.82