Word metric
In group theory, a branch of mathematics, a word metric on a group 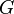 is a way to measure distance between any two elements of
is a way to measure distance between any two elements of 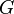 . As the name suggests, the word metric is a metric on
. As the name suggests, the word metric is a metric on 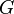 , assigning to any two elements
, assigning to any two elements  ,
, 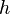 of
of 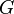 a distance
a distance 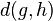 that measures how efficiently their difference
that measures how efficiently their difference 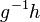 can be expressed as a word whose letters come from a generating set for the group. The word metric on G is very closely related to the Cayley graph of G: the word metric measures the length of the shortest path in the Cayley graph between two elements of G.
can be expressed as a word whose letters come from a generating set for the group. The word metric on G is very closely related to the Cayley graph of G: the word metric measures the length of the shortest path in the Cayley graph between two elements of G.
A generating set for 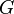 must first be chosen before a word metric on
must first be chosen before a word metric on 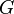 is specified. Different choices of a generating set will typically yield different word metrics. While this seems at first to be a weakness in the concept of the word metric, it can be exploited to prove theorems about geometric properties of groups, as is done in geometric group theory.
is specified. Different choices of a generating set will typically yield different word metrics. While this seems at first to be a weakness in the concept of the word metric, it can be exploited to prove theorems about geometric properties of groups, as is done in geometric group theory.
Examples
The group of integers Z
The group of integers Z is generated by the set {-1,+1}. The integer -3 can be expressed as -1-1-1+1-1, a word of length 5 in these generators. But the word which expresses -3 most efficiently is -1-1-1, a word of length 3. The distance between 0 and -3 in the word metric is therefore equal to 3. More generally, the distance between two integers m and n in the word metric is equal to |m-n|, because the shortest word representing the difference m-n has length equal to |m-n|.
The group 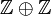
For a more illustrative example, the elements of the group 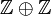 can be thought of as vectors in the Cartesian plane with integer coefficients. The group
can be thought of as vectors in the Cartesian plane with integer coefficients. The group 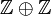 is generated by the standard unit vectors
is generated by the standard unit vectors  ,
, 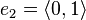 and their inverses
and their inverses 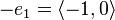 ,
, 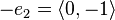 . The Cayley graph of
. The Cayley graph of 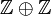 is the so-called taxicab geometry. It can be pictured in the plane as an infinite square grid of city streets, where each horizontal and vertical line with integer coordinates is a street, and each point of
is the so-called taxicab geometry. It can be pictured in the plane as an infinite square grid of city streets, where each horizontal and vertical line with integer coordinates is a street, and each point of 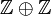 lies at the intersection of a horizontal and a vertical street. Each horizontal segment between two vertices represents the generating vector
lies at the intersection of a horizontal and a vertical street. Each horizontal segment between two vertices represents the generating vector 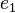 or
or 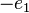 , depending on whether the segment is travelled in the forward or backward direction, and each vertical segment represents
, depending on whether the segment is travelled in the forward or backward direction, and each vertical segment represents 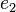 or
or 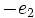 . A car starting from
. A car starting from 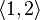 and travelling along the streets to
and travelling along the streets to 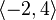 can make the trip by many different routes. But no matter what route is taken, the car must travel at least |1 - (-2)| = 3 horizontal blocks and at least |2 - 4| = 2 vertical blocks, for a total trip distance of at least 3 + 2 = 5. If the car goes out of its way the trip may be longer, but the minimal distance travelled by the car, equal in value to the word metric between
can make the trip by many different routes. But no matter what route is taken, the car must travel at least |1 - (-2)| = 3 horizontal blocks and at least |2 - 4| = 2 vertical blocks, for a total trip distance of at least 3 + 2 = 5. If the car goes out of its way the trip may be longer, but the minimal distance travelled by the car, equal in value to the word metric between 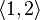 and
and 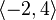 is therefore equal to 5.
is therefore equal to 5.
In general, given two elements 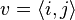 and
and 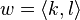 of
of 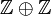 , the distance between
, the distance between 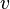 and
and 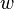 in the word metric is equal to
in the word metric is equal to 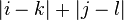 .
.
Definition
Let G be a group, let S be a generating set for G, and suppose that S is closed under the inverse operation on G. A word over the set S is just a finite sequence 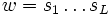 whose entries
whose entries 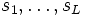 are elements of S. The integer L is called the length of the word
are elements of S. The integer L is called the length of the word 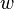 . Using the group operation in G, the entries of a word
. Using the group operation in G, the entries of a word 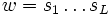 can be multiplied in order, remembering that the entries are elements of G. The result of this multiplication is an element
can be multiplied in order, remembering that the entries are elements of G. The result of this multiplication is an element 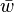 in the group G which is called the evaluation of the word w. As a special case, the empty word
in the group G which is called the evaluation of the word w. As a special case, the empty word 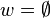 has length zero, and its evaluation is the identity element of G.
has length zero, and its evaluation is the identity element of G.
Given an element g of G, its word norm |g| with respect to the generating set S is defined to be the shortest length of a word 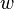 over S whose evaluation
over S whose evaluation 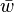 is equal to g. Given two elements g,h in G, the distance d(g,h) in the word metric with respect to S is defined to be
is equal to g. Given two elements g,h in G, the distance d(g,h) in the word metric with respect to S is defined to be 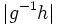 . Equivalently, d(g,h) is the shortest length of a word w over S such that
. Equivalently, d(g,h) is the shortest length of a word w over S such that 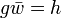 .
.
The word metric on G satisfies the axioms for a metric, and it is not hard to prove this. The proof of the symmetry axiom d(g,h) = d(h,g) for a metric uses the assumption that the generating set S is closed under inverse.
Variations
The word metric has an equivalent definition formulated in more geometric terms using the Cayley graph of G with respect to the generating set S. When each edge of the Cayley graph is assigned a metric of length 1, the distance between two group elements g,h in G is equal to the shortest length of a path in the Cayley graph from the vertex g to the vertex h.
The word metric on G can also be defined without assuming that the generating set S is closed under inverse. To do this, first symmetrize S, replacing it by a larger generating set consisting of each  in S as well as its inverse
in S as well as its inverse 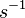 . Then define the word metric with respect to S to be the word metric with respect to the symmetrization of S.
. Then define the word metric with respect to S to be the word metric with respect to the symmetrization of S.
Example in a free group
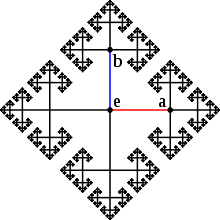
Suppose that F is the free group on the two element set 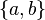 . A word w in the symmetric generating set
. A word w in the symmetric generating set 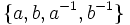 is said to be reduced if the letters
is said to be reduced if the letters 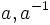 do not occur next to each other in w, nor do the letters
do not occur next to each other in w, nor do the letters 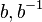 . Every element
. Every element 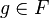 is represented by a unique reduced word, and this reduced word is the shortest word representing g. For example, since the word
is represented by a unique reduced word, and this reduced word is the shortest word representing g. For example, since the word 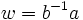 is reduced and has length 2, the word norm of
is reduced and has length 2, the word norm of 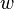 equals 2, so the distance in the word norm between
equals 2, so the distance in the word norm between 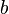 and
and 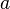 equals 2. This can be visualized in terms of the Cayley graph, where the shortest path between b and a has length 2.
equals 2. This can be visualized in terms of the Cayley graph, where the shortest path between b and a has length 2.
Theorems
Isometry of the left action
The group G acts on itself by left multiplication: the action of each 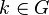 takes each
takes each 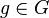 to
to 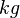 . This action is an isometry of the word metric. The proof is simple: the distance between
. This action is an isometry of the word metric. The proof is simple: the distance between 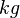 and
and 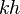 equals
equals 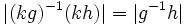 which equals the distance between
which equals the distance between 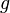 and
and 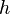 .
.
Bilipschitz invariants of a group
The word metric on a group G is not unique, because different symmetric generating sets give different word metrics. However, finitely generated word metrics are unique up to bilipschitz equivalence: if 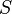 ,
, 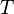 are two symmetric, finite generating sets for G with corresponding word metrics
are two symmetric, finite generating sets for G with corresponding word metrics 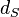 ,
, 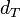 , then there is a constant
, then there is a constant 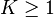 such that for any
such that for any 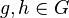 ,
,
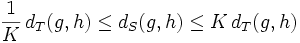 .
.
This constant K is just the maximum of the 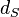 word norms of elements of
word norms of elements of 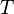 and the
and the 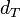 word norms of elements of
word norms of elements of 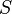 . This proof is also easy: any word over S can be converted by substitution into a word over T, expanding the length of the word by a factor of at most K, and similarly for converting words over T into words over S.
. This proof is also easy: any word over S can be converted by substitution into a word over T, expanding the length of the word by a factor of at most K, and similarly for converting words over T into words over S.
The bilipschitz equivalence of word metrics implies in turn that the growth rate of a finitely generated group is a well-defined isomorphism invariant of the group, independent of the choice of a finite generating set. This implies in turn that various properties of growth, such as polynomial growth, the degree of polynomial growth, and exponential growth, are isomorphism invariants of groups. This topic is discussed further in the article on the growth rate of a group.
Quasi-isometry invariants of a group
In geometric group theory, groups are studied by their actions on metric spaces. A principle which generalizes the bilipschitz invariance of word metrics says that any finitely generated word metric on G is quasi-isometric to any proper, geodesic metric space on which G acts, properly discontinuously and cocompactly. Metric spaces on which G acts in this manner are called model spaces for G.
It follows in turn that any quasi-isometrically invariant property satisfied by the word metric of G or by any model space of G is an isomorphism invariant of G. Modern geometric group theory is in large part the study of quasi-isometry invariants.
See also
References
- J. W. Cannon, Geometric group theory, in Handbook of geometric topology pages 261--305, North-Holland, Amsterdam, 2002, ISBN 0-444-82432-4