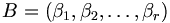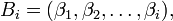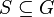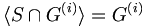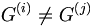Strong generating set
In abstract algebra, especially in the area of group theory, a strong generating set of a permutation group is a generating set that clearly exhibits the permutation structure as described by a stabilizer chain. A stabilizer chain is a sequence of subgroups, each containing the next and each stabilizing one more point.
Let 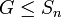 be a group of permutations of the set
be a group of permutations of the set 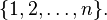 Let
Let
be a sequence of distinct integers, 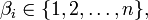 such that the pointwise stabilizer of
such that the pointwise stabilizer of 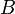 is trivial (i.e., let
is trivial (i.e., let 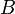 be a base for
be a base for 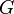 ). Define
). Define
and define 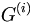 to be the pointwise stabilizer of
to be the pointwise stabilizer of 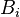 . A strong generating set (SGS) for G relative to the base
. A strong generating set (SGS) for G relative to the base 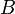 is a set
is a set
such that
for each 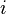 such that
such that 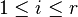 .
.
The base and the SGS are said to be non-redundant if
for 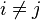 .
.
A base and strong generating set (BSGS) for a group can be computed using the Schreier–Sims algorithm.
References
- A. Seress, Permutation Group Algorithms, Cambridge University Press, 2002.