Deltoidal icositetrahedron
| Deltoidal icositetrahedron | |
|---|---|
 Animated | |
| Type | Catalan |
| Conway notation | oC or deC |
| Coxeter diagram | |
| Face polygon |  kite |
| Faces | 24 |
| Edges | 48 |
| Vertices | 26 = 6 + 8 + 12 |
| Face configuration | V3.4.4.4 |
| Symmetry group | Oh, BC3, [4,3], *432 |
| Rotation group | O, [4,3]+, (432) |
| Dihedral angle | 138°07′05″ arccos(−7 + 4√2/17) |
| Dual polyhedron | rhombicuboctahedron |
| Properties | convex, face-transitive |
 Net | |
In geometry, a deltoidal icositetrahedron (also a trapezoidal icositetrahedron, tetragonal icosikaitetrahedron,[1] and strombic icositetrahedron) is a Catalan solid which looks a bit like an overinflated cube. Its dual polyhedron is the rhombicuboctahedron.
Dimensions
The 24 faces are kites. The short and long edges of each kite are in the ratio 1:(2 − 1/√2) ≈ 1:1.292893...
If its smallest edges have length 1, its surface area is and its volume is .
Occurrences in nature and culture
The deltoidal icositetrahedron is a crystal habit often formed by the mineral analcime and occasionally garnet. The shape is often called a trapezohedron in mineral contexts, although in solid geometry that name has another meaning.
Orthogonal projections
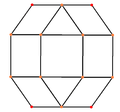
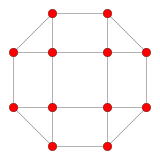
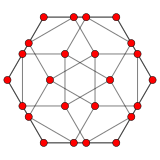
The deltoidal icositetrahedron has three symmetry positions, all centered on vertices:
| Projective symmetry |
[2] | [4] | [6] |
|---|---|---|---|
| Image |  |
 |
 |
| Dual image |
 |
 |
 |
Related polyhedra
The great triakis octahedron is a stellation of the deltoidal icositetrahedron.
Dyakis dodecahedron
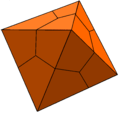
The deltoidal icositetrahedron is topologically equivalent to a cube whose faces are divided in quadrants. It can also be projected onto a regular octahedron, with kite faces, or more general quadrilaterals with pyritohedral symmetry. In Conway polyhedron notation, they represent an ortho operation to a cube or octahedron.
In crystallography a rotational variation is called a dyakis dodecahedron[2][3] or diploid.[4]
| Octahedral, Oh, order 24 | Pyritohedral, Th, order 12 | |||
|---|---|---|---|---|
 |
 |
 |
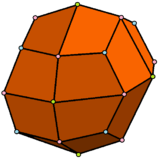 |
 |
Related polyhedra and tilings

The deltoidal icositetrahedron is one of a family of duals to the uniform polyhedra related to the cube and regular octahedron.
| Uniform octahedral polyhedra | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
||||||||
| Duals to uniform polyhedra | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
This polyhedron is topologically related as a part of sequence of deltoidal polyhedra with face figure (V3.4.n.4), and continues as tilings of the hyperbolic plane. These face-transitive figures have (*n32) reflectional symmetry.
| Symmetry *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | ||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] | |
| Figure Config. |
 V3.4.2.4 |
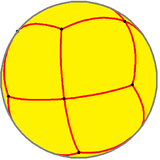 V3.4.3.4 |
 V3.4.4.4 |
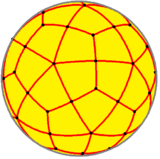 V3.4.5.4 |
 V3.4.6.4 |
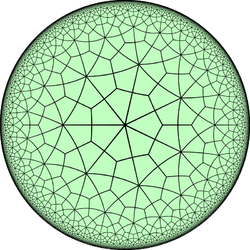 V3.4.7.4 |
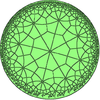 V3.4.8.4 |
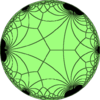 V3.4.∞.4 |
See also
- Deltoidal hexecontahedron
- Tetrakis hexahedron, another 24-face Catalan solid which looks a bit like an overinflated cube.
- "The Haunter of the Dark", a story by H.P. Lovecraft, whose plot involves this figure
References
- ↑ Conway, Symmetries of Things, p.284–286
- ↑ Isohedron 24k
- ↑ The Isometric Crystal System
- ↑ https://www.uwgb.edu/dutchs/symmetry/xlforms.htm
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 730208 (The thirteen semiregular convex polyhedra and their duals, Page 23, Deltoidal icositetrahedron)
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 286, tetragonal icosikaitetrahedron)
External links
- Eric W. Weisstein, Deltoidal icositetrahedron (Catalan solid) at MathWorld.
- Deltoidal (Trapezoidal) Icositetrahedron – Interactive Polyhedron model