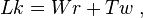Ribbon (mathematics)
In mathematics (differential geometry) by a ribbon (or strip) 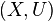 is meant a smooth space curve
is meant a smooth space curve 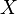 given by a three-dimensional vector
given by a three-dimensional vector 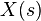 , depending continuously on the curve arc-length
, depending continuously on the curve arc-length  (
(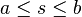 ), together with a smoothly varying unit vector
), together with a smoothly varying unit vector 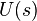 perpendicular to
perpendicular to 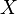 at each point (Blaschke 1950).
at each point (Blaschke 1950).
The ribbon 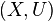 is called simple and closed if
is called simple and closed if 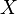 is simple (i.e. without self-intersections) and closed and if
is simple (i.e. without self-intersections) and closed and if 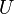 and all its derivatives agree at
and all its derivatives agree at 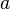 and
and 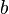 .
For any simple closed ribbon the curves
.
For any simple closed ribbon the curves 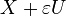 given parametrically by
given parametrically by 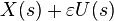 are, for all sufficiently small positive
are, for all sufficiently small positive  , simple closed curves disjoint from
, simple closed curves disjoint from 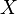 .
.
The ribbon concept plays an important role in the Cǎlugǎreǎnu-White-Fuller formula (Fuller 1971), that states that
where 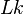 is the asymptotic (Gauss) linking number (a topological quantity),
is the asymptotic (Gauss) linking number (a topological quantity), 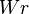 denotes the total writhing number (or simply writhe) and
denotes the total writhing number (or simply writhe) and 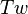 is the total twist number (or simply twist).
is the total twist number (or simply twist).
Ribbon theory investigates geometric and topological aspects of a mathematical reference ribbon associated with physical and biological properties, such as those arising in topological fluid dynamics, DNA modeling and in material science.
References
- Blaschke, W. (1950) Einführung in die Differentialgeometrie. Springer-Verlag. ISBN 9783817115495
- Fuller, F.B. (1971) The writhing number of a space curve. PNAS USA 68, 815-819.