Resolution inference
In propositional logic, a resolution inference is an instance of the following rule:[1]
We call:
- The clauses
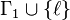 and
and 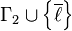 are the inference’s premises
are the inference’s premises -
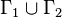 (the resolvent of the premises) is its conclusion.
(the resolvent of the premises) is its conclusion. - The literal
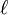 is the left resolved literal,
is the left resolved literal, - The literal
 is the right resolved literal,
is the right resolved literal, -
 is the resolved atom or pivot.
is the resolved atom or pivot.
This rule can be generalized to first-order logic to:[2]
where 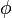 is a most general unifier of
is a most general unifier of  and
and 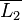 and
and 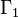 and
and 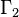 have no common variables.
have no common variables.
Example
The clauses 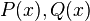 and
and 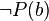 can apply this rule with
can apply this rule with ![[b/x]](../I/m/d7bac402c30ac9c64fb824c309026aec.png) as unifier.
as unifier.
Here x is a variable and b is a constant.
Here we see that
- The clauses
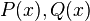 and
and 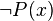 are the inference’s premises
are the inference’s premises -
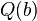 (the resolvent of the premises) is its conclusion.
(the resolvent of the premises) is its conclusion. - The literal
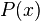 is the left resolved literal,
is the left resolved literal, - The literal
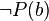 is the right resolved literal,
is the right resolved literal, -
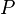 is the resolved atom or pivot.
is the resolved atom or pivot. -
![[b/x]](../I/m/d7bac402c30ac9c64fb824c309026aec.png) is the most general unifier of the resolved literals.
is the most general unifier of the resolved literals.
Notes
This article is issued from Wikipedia - version of the 5/18/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
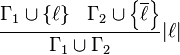
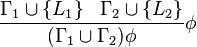
![\frac{P(x),Q(x) \,\,\,\, \neg P(b)}
{Q(b)}[b/x]](../I/m/991a96fee236a311575e5f26369ab3c0.png)