Rectified truncated tetrahedron

Rectified truncated tetrahedron
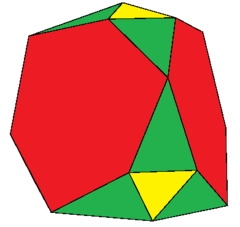Schläfli symbol	rt{3,3}
Conway notation	atT
Faces	20: 4 {3} 12 { }∨( ) 4 {6}
Edges	48
Vertices	12+18
Symmetry group	Td, [3,3], (*332) order 24
Rotation group	T, [3,3]+, (332), order 12
Dual polyhedron	Joined truncated tetrahedron
Properties	convex
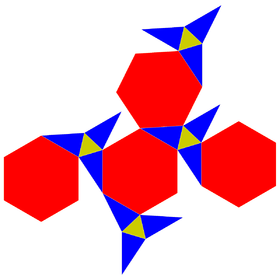Net

The rectified truncated tetrahedron is a polyhedron, constructed as a rectified truncated tetrahedron. It has 20 faces: 4 equilateral triangles, 12 isosceles triangles, and 4 regular hexagons.

Related polyhedra

The rectified truncated tetrahedron can be seen in sequence of rectification and truncation operations from the tetrahedron. Further truncation, and alternation operations creates two more polyhedra:

Name	Truncated tetrahedron	Rectified truncated tetrahedron	Truncated rectified truncated tetrahedron	Snub rectified truncated tetrahedron
Coxeter	tT	rtT	trtT	srtT
Conway		atT	btT	stT
Image
Conway	dtT = kT	jtT	mtT	gtT
Dual

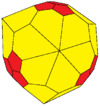See also

• Rectified truncated cube
• Rectified truncated octahedron
• Rectified truncated dodecahedron
• Rectified truncated icosahedron

References

• Coxeter Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (pp. 145–154 Chapter 8: Truncation)
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5

External links

• George Hart's Conway interpreter: generates polyhedra in VRML, taking Conway notation as input