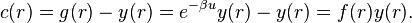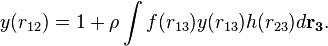Percus–Yevick approximation
In statistical mechanics the Percus–Yevick approximation[1] is a closure relation to solve the Ornstein–Zernike equation. It is also referred to as the Percus–Yevick equation. It is commonly used in fluid theory to obtain e.g. expressions for the radial distribution function.
Derivation
The direct correlation function represents the direct correlation between two particles in a system containing N − 2 other particles. It can be represented by
where 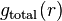 is the radial distribution function, i.e.
is the radial distribution function, i.e. ![g(r)=\exp[-\beta w(r)]](../I/m/04eb0f45582acc6ccd08133edaadd7b9.png) (with w(r) the potential of mean force) and
(with w(r) the potential of mean force) and 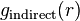 is the radial distribution function without the direct interaction between pairs
is the radial distribution function without the direct interaction between pairs 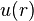 included; i.e. we write
included; i.e. we write ![g_{\rm indirect}(r)=\exp^{-\beta[w(r)-u(r)]}](../I/m/c0a131ad1f29ac5b2d1762878419d91d.png) . Thus we approximate c(r) by
. Thus we approximate c(r) by
If we introduce the function 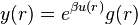 into the approximation for c(r) one obtains
into the approximation for c(r) one obtains
This is the essence of the Percus–Yevick approximation for if we substitute this result in the Ornstein–Zernike equation, one obtains the Percus–Yevick equation:
The approximation was defined by Percus and Yevick in 1958. For hard spheres, the equation has an analytical solution.[2]
See also
- Hypernetted chain equation — another closure relation
References
- ↑ Percus, Jerome K. and Yevick, George J. Analysis of Classical Statistical Mechanics by Means of Collective Coordinates. Phys. Rev. 1958, 110, 1, DOI: 10.1103/PhysRev.110.1
- ↑ Wertheim, M. S. Exact Solution of the Percus-Yevick Integral Equation for Hard Spheres. Phys. Rev. Lett. 1963, 10, 321-323, DOI: 10.1103/PhysRevLett.10.321
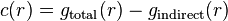
![c(r)=e^{-\beta w(r)}- e^{-\beta[w(r)-u(r)]}. \,](../I/m/e99490280cb261efe958b3e8c5eeee93.png)