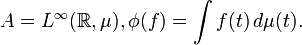Free independence

In the mathematical theory of free probability, the notion of free independence was introduced by Dan Voiculescu.^[1] The definition of free independence is parallel to the classical definition of independence, except that the role of Cartesian products of measure spaces (corresponding to tensor products of their function algebras) is played by the notion of a free product of (non-commutative) probability spaces.

In the context of Voiculescu's free probability theory, many classical-probability theorems or phenomena have free probability analogs: the same theorem or phenomenon holds (perhaps with slight modifications) if the classical notion of independence is replaced by free independence. Examples of this include: the free central limit theorem; notions of free convolution; existence of free stochastic calculus and so on.

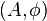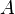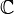Let $(A,\phi)$ be a non-commutative probability space, i.e. a unital algebra $A$ over $\mathbb{C}$ equipped with a unital linear functional 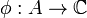$\phi:A\to\mathbb{C}$ . As an example, one could take, for a probability measure $\mu$ ,

A = L^\infty(\mathbb{R},\mu),\phi(f) = \int f(t)\,d\mu(t).

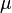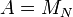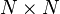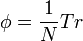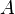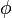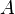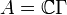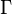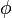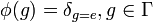Another example may be $A=M_N$ , the algebra of $N\times N$ matrices with the functional given by the normalized trace $\phi=\frac{1}{N}Tr$ . Even more generally, $A$ could be a von Neumann algebra and $\phi$ a state on $A$ . A final example is the group algebra $A=\mathbb{C}\Gamma$ of a (discrete) group $\Gamma$ with the functional $\phi$ given by the group trace $\phi (g) = \delta_{g=e},g\in \Gamma$ .

Let 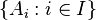$\{A_i : i\in I\}$ be a family of unital subalgebras of $A$ .

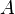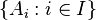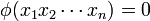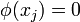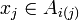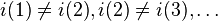Definition. The family $\{A_i : i\in I\}$ is called freely independent if $\phi(x_1 x_2 \cdots x_n) =0$ whenever $\phi(x_j)=0$ , $x_j \in A_{i(j)}$ and $i(1)\neq i(2), i(2)\neq i(3),\dots$ .

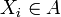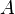If $X_i\in A$ , $i\in I$ is a family of elements of $A$ (these can be thought of as random variables in 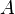$A$ ), they are called

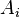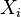freely independent if the algebras $A_i$ generated by $1$ and $X_i$ are freely independent.

Examples of free independence

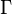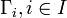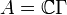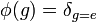Let $\Gamma$ be the free product of groups $\Gamma_i,i\in I$ , let $A=\mathbb{C}\Gamma$ be the group algebra, $\phi(g)=\delta_{g=e}$ be the group trace, and set 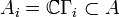$A_i=\mathbb{C}\Gamma_i\subset A$ . Then 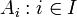$A_i:i\in I$ are freely independent.
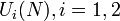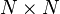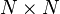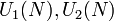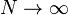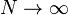Let $U_i(N),i=1,2$ be $N\times N$ unitary random matrices, taken independently at random from the $N\times N$ unitary group (with respect to the Haar measure). Then $U_1(N),U_2(N)$ become asymptotically freely independent as $N\to\infty$ . (Asymptotic freeness means that the definition of freeness holds in the limit as $N\to\infty$ ).
More generally, independent random matrices tend to be asymptotically freely independent, under certain conditions.

References

↑ D. Voiculescu, K. Dykema, A. Nica, "Free Random Variables", CIRM Monograph Series, AMS, Providence, RI, 1992

This article is issued from Wikipedia - version of the 4/1/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.