Ehrenfest equations
Ehrenfest equations (named after Paul Ehrenfest) are equations which describe changes in specific heat capacity and derivatives of specific volume in second-order phase transitions. The Clausius–Clapeyron relation does not make sense for second-order phase transitions,[1] as both specific heat capacity and specific volume do not change in second-order phase transitions.
Quantitative consideration
Ehrenfest equations are the consequence of continuity of specific entropy  and specific volume
and specific volume 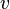 , which are first derivatives of specific Gibbs free energy – in second-order phase transitions. If one considers specific entropy
, which are first derivatives of specific Gibbs free energy – in second-order phase transitions. If one considers specific entropy  as a function of temperature and pressure, then its differential is:
as a function of temperature and pressure, then its differential is:
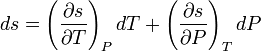 .
As
.
As 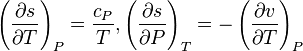 , then the differential of specific entropy also is:
, then the differential of specific entropy also is:
 ,
,
where 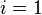 and
and 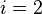 are the two phases which transit one into other. Due to continuity of specific entropy, the following holds in second-order phase transitions:
are the two phases which transit one into other. Due to continuity of specific entropy, the following holds in second-order phase transitions: 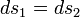 . So,
. So,
![\left( {c_{2P} - c_{1P} } \right){{dT} \over T} = \left[ {\left( {{{\partial v_2 } \over {\partial T}}} \right)_P - \left( {{{\partial v_1 } \over {\partial T}}} \right)_P } \right]dP](../I/m/8cf14d4362e0200c1024a807016491af.png)
Therefore, the first Ehrenfest equation is:
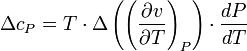 .
.
The second Ehrenfest equation is got in a like manner, but specific entropy is considered as a function of temperature and specific volume:
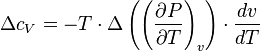
The third Ehrenfest equation is got in a like manner, but specific entropy is considered as a function of 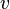 и
и 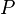 :
:
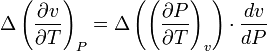 .
.
Continuity of specific volume as a function of 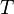 and
and 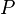 gives the fourth Ehrenfest equation:
gives the fourth Ehrenfest equation:
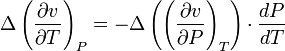 .
.
Application
Derivatives of Gibbs free energy are not always finite. Transitions between different magnetic states of metals can't be described by Ehrenfest equations.
See also
References
- ↑ Sivuhin D.V. General physics course. V.2. Thermodynamics and molecular physics. 2005