Cuthill–McKee algorithm


In the mathematical subfield of matrix theory, the Cuthill–McKee algorithm (CM), named for Elizabeth Cuthill and J. McKee ,[1] is an algorithm to permute a sparse matrix that has a symmetric sparsity pattern into a band matrix form with a small bandwidth. The reverse Cuthill–McKee algorithm (RCM) due to Alan George is the same algorithm but with the resulting index numbers reversed. In practice this generally results in less fill-in than the CM ordering when Gaussian elimination is applied.[2]
The Cuthill McKee algorithm is a variant of the standard breadth-first search
algorithm used in graph algorithms. It starts with a peripheral node and then
generates levels 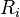 for
for 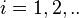 until all nodes
are exhausted. The set
until all nodes
are exhausted. The set  is created from set
is created from set 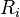 by listing all vertices adjacent to all nodes in
by listing all vertices adjacent to all nodes in 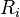 . These
nodes are listed in increasing degree. This last detail is the only difference
with the breadth-first search algorithm.
. These
nodes are listed in increasing degree. This last detail is the only difference
with the breadth-first search algorithm.
Algorithm
Given a symmetric 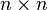 matrix we visualize the matrix as the adjacency matrix of a graph. The Cuthill–McKee algorithm is then a relabeling of the vertices of the graph to reduce the bandwidth of the adjacency matrix.
matrix we visualize the matrix as the adjacency matrix of a graph. The Cuthill–McKee algorithm is then a relabeling of the vertices of the graph to reduce the bandwidth of the adjacency matrix.
The algorithm produces an ordered n-tuple R of vertices which is the new order of the vertices.
First we choose a peripheral vertex (the vertex with the lowest degree) x and set R := ({x}).
Then for 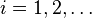 we iterate the following steps while |R| < n
we iterate the following steps while |R| < n
- Construct the adjacency set
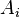 of
of 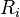 (with
(with 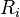 the i-th component of R) and exclude the vertices we already have in R
the i-th component of R) and exclude the vertices we already have in R
- Sort
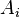 with ascending vertex order (vertex degree).
with ascending vertex order (vertex degree). - Append
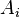 to the Result set R.
to the Result set R.
In other words, number the vertices according to a particular breadth-first traversal where neighboring vertices are visited in order from lowest to highest vertex order.
See also
References
- ↑ E. Cuthill and J. McKee. Reducing the bandwidth of sparse symmetric matrices In Proc. 24th Nat. Conf. ACM, pages 157–172, 1969.
- ↑ J. A. George and J. W-H. Liu, Computer Solution of Large Sparse Positive Definite Systems, Prentice-Hall, 1981
- Cuthill–McKee documentation for the Boost C++ Libraries.
- A detailed description of the Cuthill–McKee algorithm.
- symrcm MATLAB's implementation of RCM.
- reverse_cuthill_mckee RCM routine from SciPy written in Cython.